
The first thing to say about this is that Gnu 2-ply is not very good at assessing this type of position. It does mark this as a substantial error, but the rollout marks this is being a very marginal double/no double, with Black winning the match about 93.25% whether he doubles or not. As White might pass, I suppose that doubling figures to be correct, because a pass will take Black to Crawford - needs 9 where his equity will be about 94.5% according to the MET that I use. If Black is the weaker player he should definitely cube, as the position is entirely skill free.
Extreme Gammon agrees with these figures.
So, don't ever take a bot evaluation as gospel. Always check it if you are interested in the position.
Nr Nonnymouse got it right. This is just about a redouble and a correct take, but I would imagine that many players would be very reluctant to turn the cube here and risk an 8 point loss when they can only win 3. Black is actually a 90% favourite to win here, so how would one arrive at the correct decision over the board? We do a risk/gain analysis.
Note that for this, I round all percentages down to the nearest whole number to make the arithmetic easier and I assume when I say "Black no double" that he never doubles. In practice he will do a bit better than this figure if he redoubles correctly later. Of course White always redoubles to 8 immediately.
If Black doesn't redouble and wins, he gets to Crawford - needs 9, ME= 94%
If Black redoubles and wins, he wins the match, ME = 100%
We can see that Black stands to gain 6% by doubling.
If Black doesn't redouble and loses, he gets to needs 3 - needs 7, ME = 76%
If Black redoubles and loses, he gets to needs 3 - Crawford, ME = 25%
We can see that Black risks losing 51% by doubling.
So, Risk/ Risk + Gain = 51/51 + 6 = 51/57 or 89.5%.
Balck needs to be a 90% favourite to redouble and that is almost what he has.
Can you do this in your head over the board? Very strong players can. It depends on being able to put a very exact figure on Black's game wiining chances, which in itself is very hard and then being able to remember your Match Equity Table.
Memorising Match Equity Tables is very hard for anybody. Kit Woolsey says that he can't even remember his own, although I am sure that he knows all the figures for shorter matches. For this reason, most players rely on an approximation and the most popular is Neil's Numbers.
It looks like this.
The leader's percent probability of winning the match is 50, plus the number of points by which he leads multiplied by Neil's number. Look at the top line to see how many points the trailer needs and the appropriate Neil's Number is underneath it. Some of the numbers don't have a whole number, so you have to fill that in for yourself. As originally designed, the user was intended to extrapolate, so for example the number for trailer needs 7 would be 6.5.
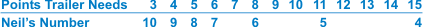
This handy gadget was designed by Neil Kazaross about 20 years ago ans is startlingly accurate even when compared to today's computer generated tables. However, don't use it when the leader only needs one or two points to win as it breaks down there, but these lines are quite easy to learn anyway.
One can of course use pencil and paper when playing online which helps and also have a printout of a match equity table to hand. Don't do this when playing a human. It isn't fair and it is cheating and you will feel very sneaky after doing it. However, if you do use a pencil and paper for your calculation when playing a bot, you will be learning how to do it until the day when you can do it mentally. The small fraction of a rating point that you might gain by this doesn't matter much, if at all!
Tomorrow, I want to look at some 4-away, 2-away positions. Until then, enjoy the game!
1 comment:
Neil has an updated chart which you can view here.
Post a Comment